Graceful Graphs
by Michael Brundage Created: 01 Mar 1993 Updated: 22 May 2014
Introduction
In 1993, in an undergraduate Caltech seminar course taught by (then postdoc) Hunter Snevily that I took, the students were encouraged to hunt around and find something interesting to research. After some hours digging through math journals in the library, I stumbled across the topic of graceful graphs.
A graceful graph is a graph whose vertices are labeled with distinct values between 0 and \(\lvert E \rvert\) (the number of edges), each edge is labelled with the absolute difference of its vertex endpoints, and as a result every edge label between 1 and \(\lvert E \rvert\) appears exactly once.
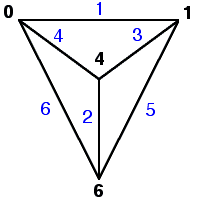
Graceful graphs have many unsolved questions that are simple to state but apparently difficult to prove. Chief among these are:
An extensive list of unsolved problems and progress on graceful and other graph labelings can be found in Joseph Gallian’s A Dynamic Survey of Graph Labelling
Graceful graphs lend themselves naturally to computational approaches. I’ve written several programs to explore this space. Often, from a few labelled instances one can find and prove a generic pattern.
Project Pages
- Enumerating all graceful graphs
- Graceful labelings of the generalized cone graphs
- Almost graceful labelings
- Ideas related to graceful graphs